Pros and cons of using premium financing
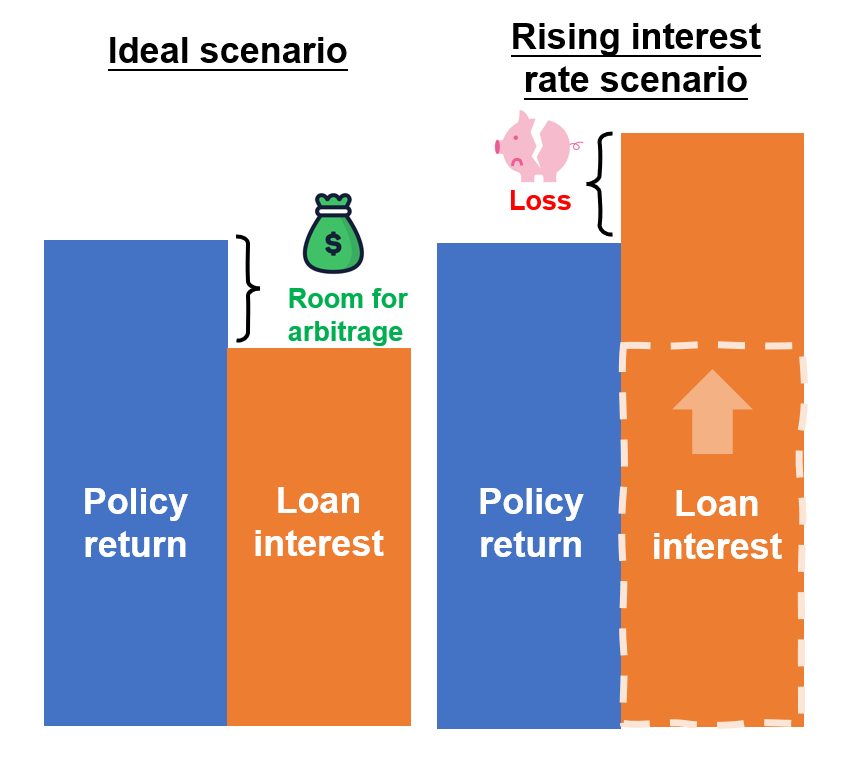
Premium financing is a wealth and liquidity management tool that, in an ideal scenario, can bring various benefits to the policy holders. For example, policy holders can, through the use of leveraging and borrowing up to 80-90% of the required premium (subject to the individual insurance product and /or financial institution), scale up their insurance policy value with the same amount of principal. So long as the policy return is greater than the loan interest, the policy holders can profit from the spread, or in other words, profit from the interest arbitrage.

In reality however, the borrowing cost and/or the policy return are generally not fixed nor guaranteed. Any fluctuations in the borrowing cost and policy return can narrow the spread for arbitrage, to an extent that may even result in a significant loss. Therefore, policy holders should not focus only on the benefits and overlook the risks and the possible adverse impact from premium financing. To facilitate your understanding and to illustrate the pros and cons on the use of premium financing, we have prepared two examples below. Please be aware that the examples have been simplified and are for illustrative purposes only. The actual circumstances will vary depending on the terms and conditions of the individual insurance product/loan contract/assignment agreement.
Illustrative Example 1: Single premium 3-year endowment policy with guaranteed return
In this example, the policy holder is required to pay HK$1 million premium in a lump sum when buying the policy and will receive a total of HK$1.1 million in return upon policy maturity at the end of the third policy year. The profit or loss upon surrender of the policy at different years is shown below. (Figures in all tables of this section are in HK$'000.)
| End of policy year | Premium paid | Surrender value | Net profit / loss upon surrender |
| (1) | (2) | (2) – (1) | |
| 1 | 1,000 | 900 | -100 |
| 2 | 1,000 | 1,030 | 30 |
|
3 (Maturity of the policy) |
1,000 | 1,100 | 100 |
You may be wondering how premium financing could improve the potential return for the policy holder without modifying the initial principal amount (i.e. the out-of-pocket premium from the policy holder). In this case, the policy holder can assign the policy to a financial institution for a premium financing loan and scale up the value of his/her policy considerably, and in doing so, improve the potential return. The use of a loan to increase the investment size is commonly referred to as "leveraging".
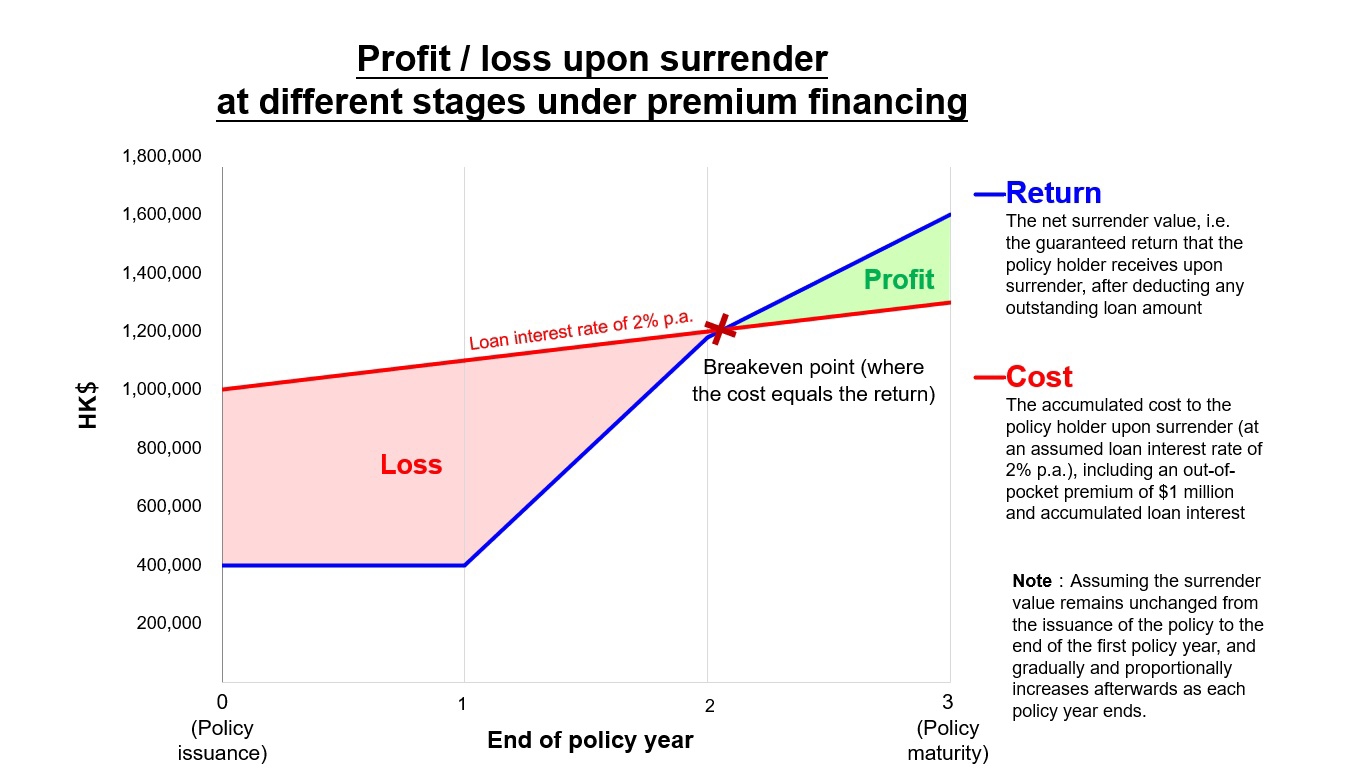
Let us explore the impact if the policy holder decides to use a 6x leverage when purchasing the same 3-year endowment policy above. In this example, the total premium is increased to $6 million, meaning that the policy holder still pays the same $1 million out-of-pocket but borrows the remaining $5 million from a financial institution. Let us further assume that the loan requires interest to be paid monthly at 2% per annum calculated using simple interest basis, and the loan principal is due only at maturity at the end of the third policy year. The results are shown below:
| End of policy year |
After scaling up the policy value with premium financing |
Outcome of the premium financing arrangement | |||||||
| Premium paid | Surrender value | Out-of-pocket premium paid |
Cumulative interest paid (Note 1) |
Net surrender value (Note 2) |
Net profit/loss upon surrender | ||||
| (1) | (2) | (3) | (4) = (1) – 5,000 | (4) – (2) – (3) | |||||
| 1 | 6,000 | 5,400 | 1,000 | 100 | 400 | -700 | |||
| 2 | 6,000 | 6,180 | 1,000 | 200 | 1,180 | -20 | |||
| 3 | 6,000 | 6,600 | 1,000 | 300 | 1,600 | 300 | |||
Note 1: The yearly interest is $100,000 (Loan principal amount of $5 million x assumed annual interest rate of 2%)
Note 2: Upon surrender, the policy holder is first required to repay the principal of $5 million to the financial institution. Therefore $5 million is deducted from the surrender value.
To better visualise the effect of premium financing, a table is prepared below to show a simple comparison. For the same out-of-pocket payment of $1 million, the policy holder through the use of premium financing now generates a net profit of $300,000 upon maturity at policy year 3 as compared to the original $100,000 without premium financing. Having said that, loss incurred upon early surrender is also magnified because of the leverage effect of premium financing and should not be overlooked.
•The leverage effect from premium financing magnifies profits as well as losses, and can turn a profit into a loss.
| End of policy year | Without premium financing | With premium financing |
| Net profit / loss upon surrender | Net profit / loss upon surrender | |
| 1 | -100 | -700 |
| 2 | 30 | -20 |
| 3 | 100 | 300 |
(click to enlarge)
Behind the profits and potential returns lurk certain risks and adverse factors that could further jeopardise the outcome of a premium financing arrangement. Policy holders should carefully consider these risks and factors before making a decision on using premium financing, for example:
- Will the interest rate for my premium financing loan increase?
- Who can make the decision to surrender my policy before maturity?
- Is the rate of return really that attractive?
- Are the policy returns guaranteed?
Will the interest rate for a premium financing loan increase?
Loan contracts for premium financing usually state that the interest rate may be subject to change depending on market circumstances and/or the financial institution has the right to adjust the rate accordingly. Any hike in the interest rate will increase the borrowing cost under premium financing and lower the return, or even worse incur losses for the policy holders.
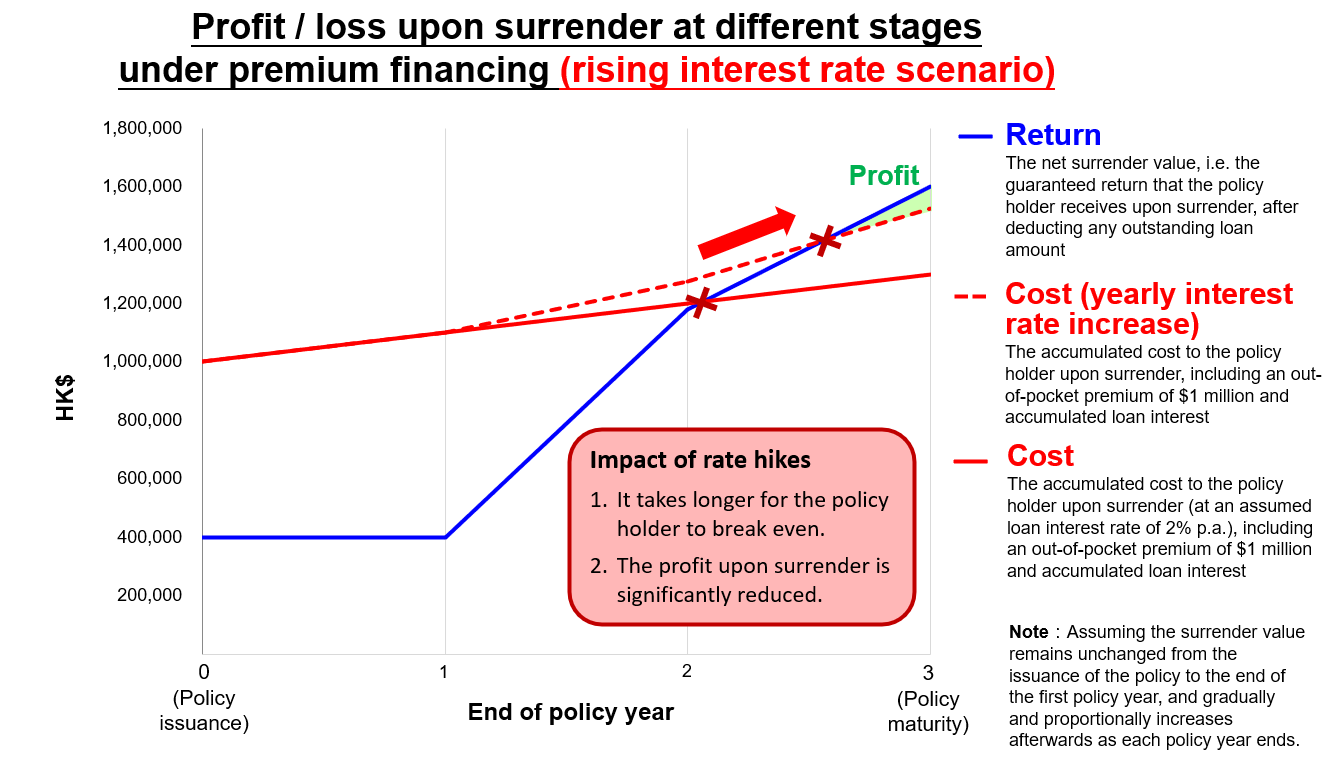
If the annual interest rate in this example is to increase year to year starting from the second policy year, how may the returns be affected? Let us look at the following table for more insight.
•Increase in interest rate reduces the profit from premium financing arrangements and amplifies any losses.
| End of policy year | Using premium financing | |||||
| Unchanged interest rate | Yearly interest rate increase | |||||
| Assumed annual interest rate |
Cumulative interest paid (Note 3) |
Net profit / loss upon surrender | Assumed annual interest rate |
Cumulative interest paid (Note 3) |
Net profit / loss upon surrender | |
| 1 | 2.0% | 100 | -700 | 2.0% | 100 | -700 |
| 2 | 2.0% | 200 | -20 | 3.5% | 275 | -95 |
| 3 | 2.0% | 300 | 300 | 5.0% | 525 | 75 |
Note 3: The yearly interest is calculated by multiplying the loan principal amount of $5 million by the respective assumed annual interest rates.
(click to enlarge)
We can see that interest rate hikes can have a tremendous impact on the return from premium financing. This is because premium financing is in essence an arbitrage, meaning that the policy holder profits from the spread when the borrowing cost is lower than the returns generated from the scaled up/leveraged policy. In a cycle of interest rate hikes however, a sharp increase in the borrowing cost may turn this profit into a loss and can be financially devastating to the policy holder under extreme circumstances.
Who can make the decision to surrender a policy before maturity?
Apart from interest rate hikes, policy holders should bear in mind that the surrender value would usually be less than the premium paid if the policy is surrendered in the early years. This difference will also be magnified under premium financing due to the leverage effect mentioned earlier.
While the above situation could be avoided if the policy holder waits patiently and holds the policy until maturity, this is true only when premium financing is NOT involved. Under a premium financing arrangement, the rights under the policy (including rights to surrender the policy) would have been assigned to the financial institution to obtain the loan. Under certain circumstances, the policy can be terminated early by the financial institution (which may result in substantial loss to the policy holder).
For example, the financial institution may ask for immediate repayment of the loan because of the following:
- The policy holder fails to meet the loan and interest payments on time;
- The policy holder's creditworthiness has changed;
- The financial institution considers that the quality of the collateral has deteriorated;
- The financial institution tightens its lending; or
- Other circumstances as applicable under the relevant loan contract.
If the policy holder does not have additional reserves to repay the loan, the financial institution can exercise its right and request the insurer to surrender the policy and settle the loan with the surrender value.
Therefore, policy holders should bear in mind that for an insurance policy purchased through the use of premium financing, the decision on whether to surrender the policy before maturity is no longer at your own discretion.
Is the rate of return really that attractive?
You may have seen promotional materials similar to the one below highlighting the return of premium financing:

The "annual average rate of return" of 10% illustrated above is actually calculated by simply deducting the total cost from the total return, and then further dividing the balance by the out-of-pocket payment of $1 million and the number of policy years ($300,000 ÷ $1 million ÷ 3 years). In this calculation, it has assumed that all the borrowing cost (including expenses like the handling fee and interest) would only be paid at maturity or upon receipt of the surrender value. In contrast, if we assume all the borrowing cost would be paid upfront and at the point of buying the policy, the principal amount will then increase from $1 million to $1.3 million, and the “annual average rate of return” will drop to 7.7% ($300,000 ÷ $1.3 million ÷ 3 years).
In reality, premium financing is a long-term arrangement. Cost and expenses payments such as the out-of-pocket premium, handling fee and monthly interest are paid at different points in time (see the graph below). The rates of return from premium financing may vary significantly depending on the timing of receipts and payments, and this variance would be more apparent if the premium financing arrangement lasts for a longer period. If the promotional materials you received include a description of the rate of return using premium financing, you should pay extra attention to the calculation methodology and the assumptions used.
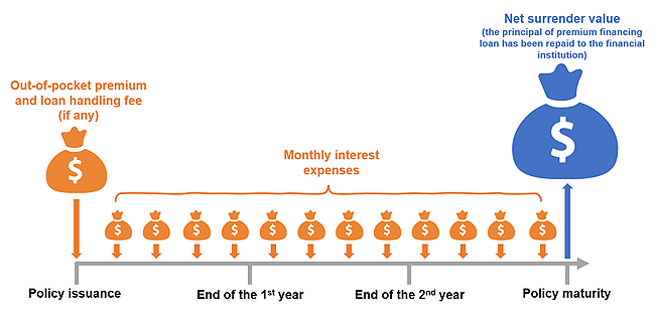
Are the policy returns guaranteed?
The policy return of the insurance product in the Illustrative Example 1 is guaranteed and must be paid to the policy holder in accordance with the contract by the insurer - nothing more and nothing less.
However, a lot of insurance products in the market have benefits covering both guaranteed and non-guaranteed components (e.g. participating policies). The non-guaranteed benefits, as the name suggests, are not guaranteed to be paid. The non-guaranteed benefits to be received are affected by the insurer's investment strategy and performance, claims experience and operational expenses, etc., which may be higher or lower than those illustrated in the benefit illustration. Under extreme circumstances, the amount of non-guaranteed benefits may be zero.
If the non-guaranteed benefits distributed by the insurer are worse than expected, even if the borrowing cost remains unchanged, the return from premium financing will be reduced and may even result in a loss. To make matters worse, the distribution of an unsatisfactory level of non-guaranteed benefits can happen concurrently with a rise in borrowing cost, and the policy holder may face an even greater loss from this double whammy.
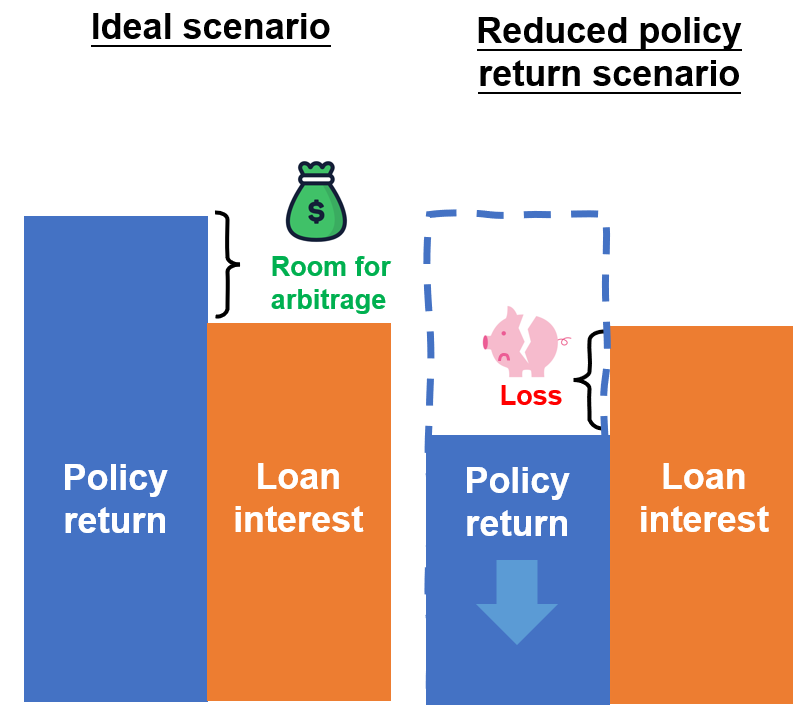
Illustrative Example 2 below demonstrates the impact of non-guaranteed benefits on a premium financing arrangement.
Illustrative Example 2: Single premium 10-year participating life insurance policy
In comparison, this product has a more complex structure and a longer policy term.
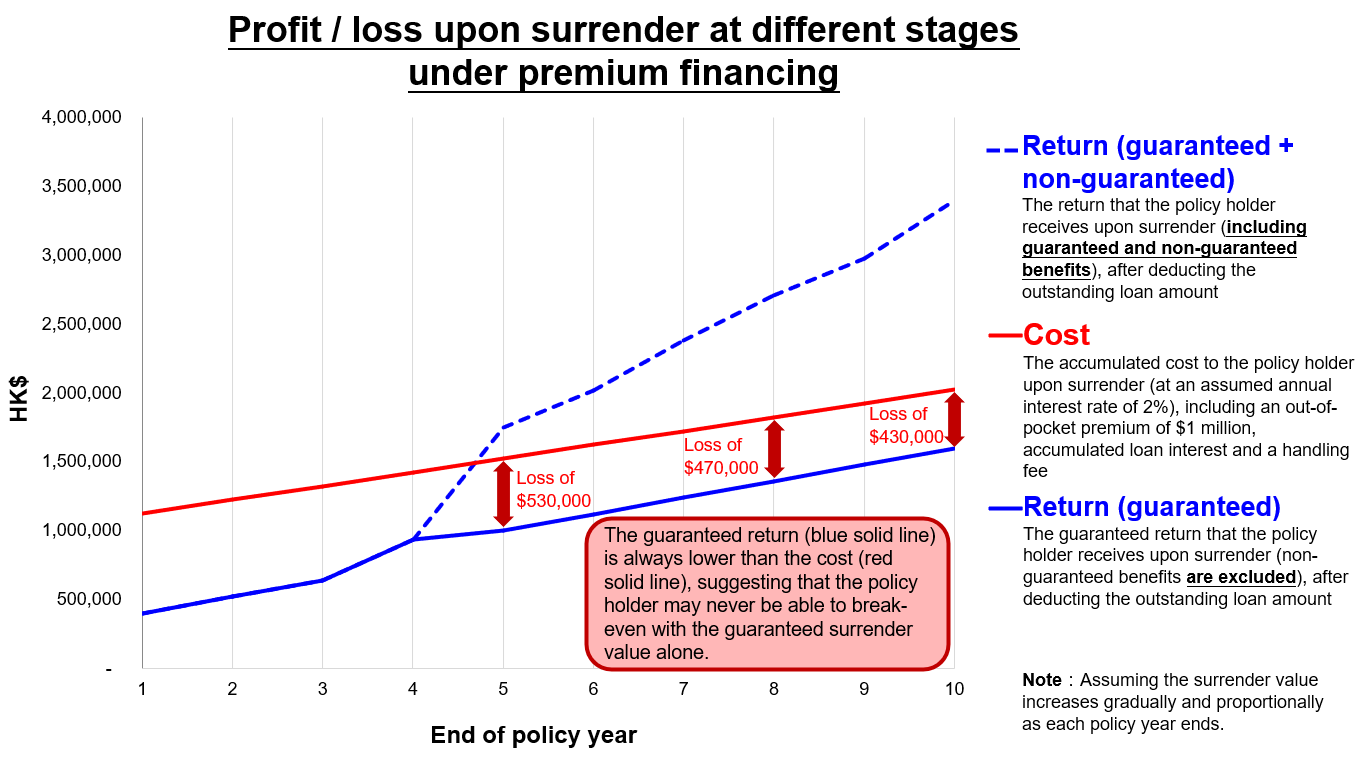
In this example, the policy holder also needs to pay a lump sum of HK$1 million to buy the policy. If the non-guaranteed benefits are distributed as illustrated, the policy holder will receive some return in the later years of the policy (as shown in the orange boxes). If, however, the non-guaranteed benefits drop to zero, the return will decrease substantially (as shown in the blue boxes). If the policy is surrendered in its early years, a loss will be incurred.
| End of policy year | Premium paid | Surrender value |
Net profit / loss upon surrender |
|||
| Guaranteed | Non-guaranteed | Total | Guaranteed | Total | ||
| (1) | (2) | (3) | (4) = (2) + (3) | (2) – (1) | (4) – (1) | |
| 1 | 1,000 | 900 | 0 | 900 | -100 | -100 |
| 3 | 1,000 | 940 | 0 | 940 | -60 | -60 |
| 5 | 1,000 | 1,000 | 130 | 1,130 | 0 | 130 |
| 8 | 1,000 | 1,060 | 230 | 1,290 | 60 | 290 |
| 10 | 1,000 | 1,100 | 300 | 1,400 | 100 | 400 |
Let us assume the policy holder adopts a premium financing arrangement with the same 6x leverage (i.e. out-of-pocket premium of $1 million and a loan of $5 million from a financial institution) at an annual simple interest rate of 2%, with the interest repayable on a monthly basis and the loan principal is fully repaid at the end of the policy period (i.e. at the end of the tenth policy year). To obtain the loan, a lump-sum handling fee of $30,000 is also charged by the financial institution.
The following table explores how the distribution of non-guaranteed benefits by the insurer may affect the policy return in the example. Since the policy holder needs to pay the lump-sum handling fee upfront and the interest is due every month, if the insurer only distributes the guaranteed benefits but not the non-guaranteed benefits, the policy holder will NOT profit from the premium financing arrangement at all.
Net profit / loss upon surrender using premium financing
|
End of policy year |
After scaling up the policy value with premium financing |
Outcome of the premium financing arrangement | |||||||
| Premium paid | Surrender value |
Out-of-pocket premium paid |
Cumulative borrowing cost paid (Note 4) |
Net surrender value (Note 5) |
Net profit/loss upon surrender |
||||
| Guaranteed |
Total (Guaranteed and non-guaranteed) |
Guaranteed |
Total (Guaranteed and non-guaranteed) |
Guaranteed |
Total (Guaranteed and non-guaranteed) |
||||
| (1) | (2) | (3) | (4) | (5) = (1) – 5,000 | (6) = (2) – 5,000 | (5) – (3) – (4) | (6) – (3) – (4) | ||
| 1 | 6,000 | 5,400 | 5,400 | 1,000 | 130 | 400 | 400 | -730 | -730 |
| 3 | 6,000 | 5,640 | 5,640 | 1,000 | 330 | 640 | 640 | -690 | -690 |
| 5 | 6,000 | 6,000 | 6,750 | 1,000 | 530 | 1,000 | 1,750 | -530 | 220 |
| 8 | 6,000 | 6,360 | 7,710 | 1,000 | 830 | 1,360 | 2,710 | -470 | 880 |
| 10 | 6,000 | 6,600 | 8,400 | 1,000 | 1,030 | 1,600 | 3,400 | -430 | 1,370 |
Note 4: Including a lump-sum handling fee of $30,000 paid at the time of loan drawdown and the accumulated interest. The yearly interest is $100,000 (Loan principal amount of $5 million x assumed annual interest rate of 2%).
Note 5: Upon surrender, the policy holder is first required to repay the principal of $5 million to the financial institution. Therefore $5 million is deducted from the surrender value.
Comparison of returns with and without distribution of non-guaranteed benefits by the insurer
| Without premium financing | With premium financing | |||
| Non-guaranteed benefits | None | Distributed as illustrated | None | Distributed as illustrated |
| End of policy year | Net profit / loss upon surrender | Net profit / loss upon surrender | Net profit / loss upon surrender | Net profit / loss upon surrender |
| 1 | -100 | -100 | -730 | -730 |
| 3 | -60 | -60 | -690 | -690 |
| 5 | 0 | 130 | -530 | 220 |
| 8 | 60 | 290 | -470 | 880 |
| 10 | 100 | 400 | -430 | 1,370 |
(click to enlarge)
Insurance products in the market have different proportion of non-guaranteed benefits, and it is difficult to generalise the impact of the distribution of non-guaranteed benefits would have on your premium financing arrangement. Although the above example (i.e. the non-guaranteed benefits equal to zero) will only happen under extreme circumstances, policy holders should bear in mind that their returns from the premium financing arrangement could be significantly impacted by the movements of non-guaranteed benefits, particularly if the underlying insurance policy has a higher proportion of non-guaranteed benefits.
Conclusion
Premium financing is a double-edged sword. The leverage it offers can boost the policy holder’s potential return but also magnifies any potential losses. The higher the loan amount is to the total premium required, the more significant the leverage would be.
While taking full advantage of the potential benefits of premium financing, policy holders should not overlook the potential financial risks posed by leveraged borrowing and the adverse impact of assigning the policy to the financial institution. Visit Smart tips on using premium financing to learn more.